Unequal usage of codons in the coding regions appears to be a universal feature of the
genomes across the phylogenetic spectra. This bias obeys mainly to (i) the uneven usage of
the amino acids in the existing proteins and (ii) the uneven usage of synonymous codons.
The bias in the usage of the synonymous codons correlates with
the abundance of the corresponding tRNAs. The correlation is particularly
strong for highly expressed genes. Codon usage is specific of the taxonomic group, and
there exist correlation between taxonomic divergence and similarity of codon usage.
By comparing the frequency of codons in a region of an species genome
read in a given frame
with the typical frequency of codons in the species genes,
it is possible to estimate a likelihood of the region coding for a protein
in such a frame. Regions in which
codons are used with frequencies similar to the typical species
codon frequencies are likely to code for genes. This idea was first
introduced by Staden and McLahlan staden(1982).
In the practice, the likelihood
can be computed in a number of different ways.
Here we compute it as a log-likelihood ratio. Let 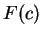 be the frequency (probability) of codon
be the frequency (probability) of codon 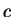 in the genes of the species
under consideration (in other words, in the genes of the species
under consideration (in other words, 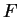 is the codon usage table,
see Table 1).
Then, given a sequence of codons is the codon usage table,
see Table 1).
Then, given a sequence of codons
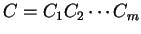 ,
and assuming independence between adjacent codons ,
and assuming independence between adjacent codons
is the probability of finding the
sequence of codons 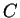 knowing that knowing that 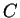 codes for a protein.
For instance, if codes for a protein.
For instance, if 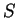 is the sequence
S= AGGACG,
when read in frame 1, it results in the sequence is the sequence
S= AGGACG,
when read in frame 1, it results in the sequence
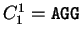 , ,
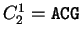 . Then . Then
Substituting the appropriate values from Table 1,
we obtain
On the other hand, let 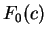 be the frequency of
codon be the frequency of
codon 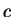 in a non-coding sequence. in a non-coding sequence.
is the probability of
finding the sequence  if if 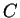 is non-coding.
Assuming the random model of coding DNA, is non-coding.
Assuming the random model of coding DNA,
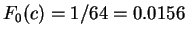 for all codons, and for all codons, and 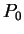 for the above sequence of codons
for the above sequence of codons 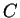 would be would be
The log-likelihood ratio for 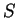 coding in frame coding in frame  , ,  ,
is ,
is
The log-likelihood ratios for 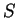 coding in frames coding in frames 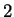 , and , and 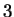 (
(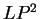 and and 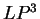 ) are computed in a similar way.
As it can be seen, in this case
the log-likelihood ratio ) are computed in a similar way.
As it can be seen, in this case
the log-likelihood ratio 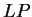 is indeed greater than zero in the
coding frame of the exon sequence, while is smaller than zero in
the non-coding frames of the exon sequence and in all frames of the intron
sequence. is indeed greater than zero in the
coding frame of the exon sequence, while is smaller than zero in
the non-coding frames of the exon sequence and in all frames of the intron
sequence.
In the practice, the problem is not usually to determine the
likelihood that a given sequence is coding or not, but to locate the
(usually small) coding regions within large genomic sequences.
The typical procedure is to compute the value of a coding
statistic in successive (usually overlapping) windows (an sliding window),
and record the
value of the statistic for each of the windows. This generates a profile
along the sequence in which peaks may point to the coding regions and valleys
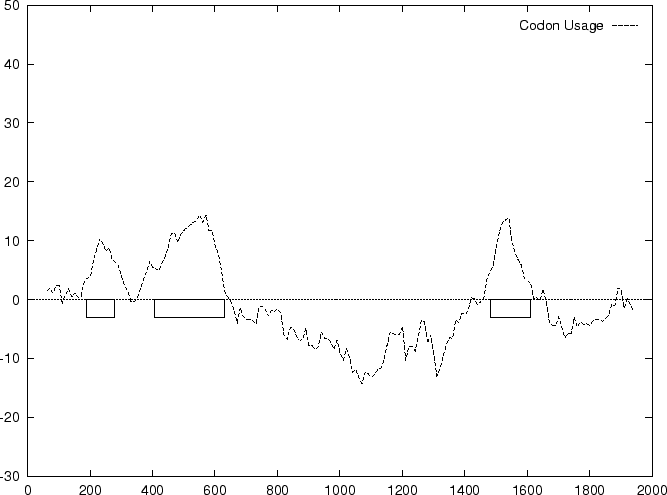
to the non-coding ones. In Figure 1,
we plot the result of sliding a window
of length 120 bp, the distance between consecutive windows being 10 bp,
computing 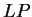 in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human
 -globin gene. -globin gene.
Table 1:
The human codon usage and codon preference table as published in
Weizmann Institute of Science. For each
codon, the table displays the frequency of usage of each codon (per thousand)
in human coding regions (first column) and the relative frequency of each
codon among synonymous codons (second column).
| The Human Codon Usage Table |
|
Gly |
GGG |
17.08 |
0.23 |
Arg |
AGG |
12.09 |
0.22 |
Trp |
TGG |
14.74 |
1.00 |
Arg |
CGG |
10.40 |
0.19 |
|
Gly |
GGA |
19.31 |
0.26 |
Arg |
AGA |
11.73 |
0.21 |
End |
TGA |
2.64 |
0.61 |
Arg |
CGA |
5.63 |
0.10 |
|
Gly |
GGT |
13.66 |
0.18 |
Ser |
AGT |
10.18 |
0.14 |
Cys |
TGT |
9.99 |
0.42 |
Arg |
CGT |
5.16 |
0.09 |
|
Gly |
GGC |
24.94 |
0.33 |
Ser |
AGC |
18.54 |
0.25 |
Cys |
TGC |
13.86 |
0.58 |
Arg |
CGC |
10.82 |
0.19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Glu |
GAG |
38.82 |
0.59 |
Lys |
AAG |
33.79 |
0.60 |
End |
TAG |
0.73 |
0.17 |
Gln |
CAG |
32.95 |
0.73 |
|
Glu |
GAA |
27.51 |
0.41 |
Lys |
AAA |
22.32 |
0.40 |
End |
TAA |
0.95 |
0.22 |
Gln |
CAA |
11.94 |
0.27 |
|
Asp |
GAT |
21.45 |
0.44 |
Asn |
AAT |
16.43 |
0.44 |
Tyr |
TAT |
11.80 |
0.42 |
His |
CAT |
9.56 |
0.41 |
|
Asp |
GAC |
27.06 |
0.56 |
Asn |
AAC |
21.30 |
0.56 |
Tyr |
TAC |
16.48 |
0.58 |
His |
CAC |
14.00 |
0.59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Val |
GTG |
28.60 |
0.48 |
Met |
ATG |
21.86 |
1.00 |
Leu |
TTG |
11.43 |
0.12 |
Leu |
CTG |
39.93 |
0.43 |
|
Val |
GTA |
6.09 |
0.10 |
Ile |
ATA |
6.05 |
0.14 |
Leu |
TTA |
5.55 |
0.06 |
Leu |
CTA |
6.42 |
0.07 |
|
Val |
GTT |
10.30 |
0.17 |
Ile |
ATT |
15.03 |
0.35 |
Phe |
TTT |
15.36 |
0.43 |
Leu |
CTT |
11.24 |
0.12 |
|
Val |
GTC |
15.01 |
0.25 |
Ile |
ATC |
22.47 |
0.52 |
Phe |
TTC |
20.72 |
0.57 |
Leu |
CTC |
19.14 |
0.20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ala |
GCG |
7.27 |
0.10 |
Thr |
ACG |
6.80 |
0.12 |
Ser |
TCG |
4.38 |
0.06 |
Pro |
CCG |
7.02 |
0.11 |
|
Ala |
GCA |
15.50 |
0.22 |
Thr |
ACA |
15.04 |
0.27 |
Ser |
TCA |
10.96 |
0.15 |
Pro |
CCA |
17.11 |
0.27 |
|
Ala |
GCT |
20.23 |
0.28 |
Thr |
ACT |
13.24 |
0.23 |
Ser |
TCT |
13.51 |
0.18 |
Pro |
CCT |
18.03 |
0.29 |
|
Ala |
GCC |
28.43 |
0.40 |
Thr |
ACC |
21.52 |
0.38 |
Ser |
TCC |
17.37 |
0.23 |
Pro |
CCC |
20.51 |
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 1:
Values of the model based Coding Statistics along the
2000 bp human  -globin gene sequence,
computed on an sliding window of length 120 and step 10. -globin gene sequence,
computed on an sliding window of length 120 and step 10.
|